PrivApprox Design

We describe the design of PrivApprox, a data analytics system for privacy-preserving stream processing. PrivApprox provides three properties: (i) $\underline{Privacy}$: zero-knowledge privacy guarantees for users, a privacy bound tighter than the state-of-the-art differential privacy; (ii) $\underline{Utility}$: an interface for data analysts to systematically explore the trade-offs between the output accuracy (with error-estimation) and query execution budget; (iii) $\underline{Latency}$: near real-time stream processing based on a scalable “synchronization-free” distributed architecture.

The key idea behind our approach is to marry two existing techniques together: namely, sampling (used in the context of approximate computing) and randomized response (used in the context of privacy-preserving analytics). The resulting marriage is complementary —it achieves stronger privacy guarantees and also improves performance, a necessary ingredient for achieving low-latency stream analytics.

System Overview

PrivApprox consists of two main phases: submitting queries and answering queries. In the first phase, an analyst submits a query (along with the execution budget) to clients via the aggregator and proxies. In the second phase, the query is answered by the clients in the reverse direction.

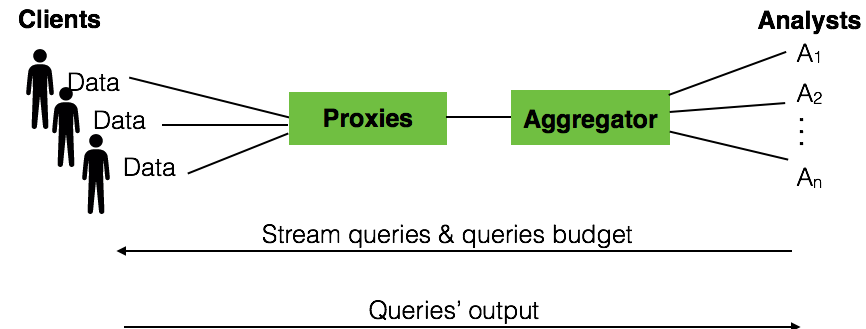
Submitting Queries

To perform statistical analysis over users’ private data streams, an analyst creates a query using the query model described in the technical report. In particular, each query consists of the following fields, and is signed by the analyst for nonrepudiation: $$\begin{equation} \label{eq:query} Query := \langle Q_{ID}, SQL, A[n], f, w, \delta \rangle \end{equation}$$

• $Q_{ID}$ denotes a unique identifier of the query. This can be generated by concatenating the identifier of the analyst with a serial number unique to the analyst.
• $SQL$ denotes the actual $SQL$ query, which is passed on to clients and executed on their respective personal data.
• $A[n]$ denotes the format of a client’s answer to the query. The answer is an n-bit vector where each bit associates with a possible answer value in the form of a “0” or “1” per index (or answer value range). $f$ denotes the answer frequency, i.e., how often the query needs to be executed at clients.
• $w$ denotes the window length for sliding window computations. For example, an analyst may only want to aggregate query results for the last 10 minutes, which means the window length is 10 minutes.
• $\delta$ denotes the sliding interval for sliding window computations. For example, an analyst may want to update the query results every one minute.

After forming the query, the analyst sends the query, along with the query execution budget, to the aggregator. Once receiving the pair of the query and query budget from the analyst, the aggregator first converts the query budget into system parameters for sampling $(s)$ and randomization $(p;q)$. Hereafter, the aggregator forwards the query and the converted system parameters to clients via proxies.

Answering Queries

After receiving the query and system parameters, we next explain how the query is answered by clients and processed by the system to produce the result for the analyst. The query answering process involves several steps including (i) sampling at clients for low-latency approximation, (ii) randomizing answers for privacy preservation, (iii) transmitting answers for anonymization and unlinkability; and finally, (iv) aggregating answers with error estimation to give a confidence level on the approximate output. We next explain the entire workflow using these four steps.

Step I: Sampling at Clients

We make use of approximate computation to achieve low-latency execution by computing over a partial subset of data items instead of the entire input dataset. Our work builds on sampling-based techniques for approximate computing proposed in the context of “Big Data” analytics. Since we aim to keep the private data stored at individual clients, PrivApprox applies an input data sampling mechanism locally at the clients. In particular, we make use of Simple Random Sampling (SRS).

Step II: Answering Queries at Clients

Next, the clients that participate in the answering process make use of randomized response to preserve privacy.

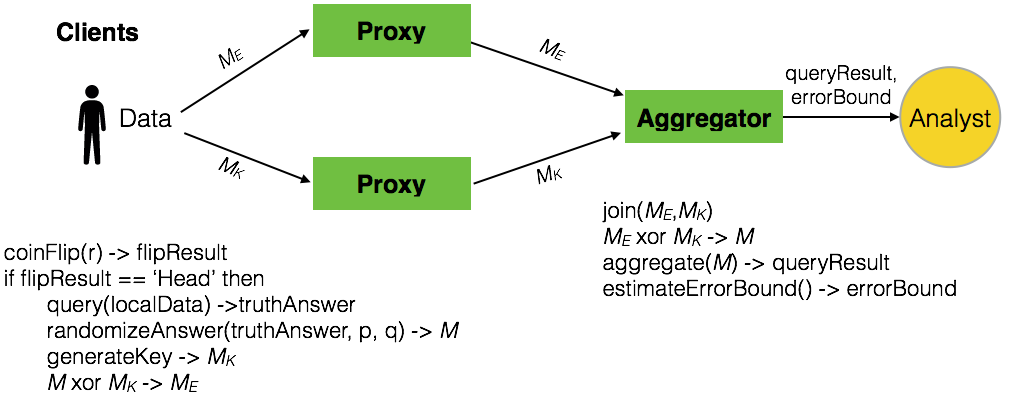
Randomized response Randomized response protects user’s privacy by allowing individuals to answer sensitive queries without providing truthful answers all the time, yet it allows analysts to collect statistical results. Randomized response works as follow: suppose an analyst sends a query to individuals to obtain statistical result about a sensitive property. To answer the query, a client locally randomizes its answer to the query. Specifically, the client flips a coin, if it comes up heads, then the client responds its truthful answer; otherwise, the client flips a second coin and responds “Yes” if it comes up heads or “No” if it comes up tails. The privacy is preserved via the ability to refuse responding truthful answers. Suppose that the probabilities of the first coin and the second coin coming up heads are $p$ and $q$, respectively. The analyst receives $N$ randomized answers from individuals, among which $R_y$ answers are “Yes”. Then, the number of original truthful “Yes” answers before the randomization process can be estimated as: $$\begin{equation} \label{eq:estimatedAnswer} E_y = \dfrac{R_y - (1- p)\times q \times N}{p} \end{equation}$$

Suppose $A_y$ and $E_y$ are the actual and the estimated numbers of the original truthful “Yes” answers, respectively. The accuracy loss $\eta$ is then defined as: $$\begin{equation} \label{eq:accuracyloss} \eta = | \dfrac{A_y - E_y}{A_y} | \end{equation}$$

It has been proven in this work that, the randomized response mechanism achieves $\epsilon$-differential privacy , where: $$\begin{equation} \label{eq:privacy-level1} \varepsilon = \ln\big(\dfrac{\Pr[Response = Yes | Truth = Yes]}{\Pr[Response = Yes | Truth = No]} \big) \end{equation}$$

More specifically, the randomized response mechanism achieves $\epsilon$-differential privacy, where: $$\begin{equation} \label{eq:privacy-level2} \varepsilon = \ln\big(\dfrac{p + (1 - p) \times q}{(1 - p) \times q}\big) \end{equation}$$

The reason is: if a truthful answer is “Yes”, then with the probability of ‘$p + (1 - p) \times q$’, the randomized answer will still remain “Yes”. Otherwise, if a truthful answer is “No”, then with the probability of ‘$(1 - p) \times q$’, the randomized answer will become “Yes”.

It is worth mentioning that, combining randomized response with the sampling technique used in Step I, we achieve not only differential privacy but also zero-knowledge privacy which is a privacy bound tighter than differential privacy. We prove our claim in Theorem C.4. in the technical report.

Step III: Transmitting Answers via Proxies

After producing randomized responses, clients transmit them to the aggregator via the proxies. To achieve anonymity and unlinkability of the clients against the aggregator and analyst, we utilize the One-Time Pad (OTP) encryption together with source rewriting, which has been proposed for anonymous communications. Under the assumptions that:

• at least two proxies are not colluding
• the proxies don’t collude with the aggregator, nor the analyst
• the aggregator and analyst have only a local view of the network

neither the aggregator, nor the analyst will learn any (pseudo-)identifier to deanonymize or link different answers to the same client. This property is achieved by source rewriting, which is a typical building block for anonymization schemes. At the same time the content of the answers is hidden from the proxies using OTP.

One-Time Pad (OTP) encryption. At a high-level, OTP employs extremely efficient bitwise XOR operations as its cryptographic primitive compared to expensive public-key cryptography. This allows us to support resource-constrained clients, e.g., smartphones and sensors. The underlying idea of OTP is quite simple: If Alice wants to send a secret message $M$ to Bob, then Alice and Bob share a secret one-time pad $M_K$ (in the form of a random bit-string of length $l$). To transmit the message $M$, Alice first converts $M$ into the form of bit-string of length $l$, and sends an encrypted message $M_E = M \oplus M_K$ to Bob, where $\oplus$ denotes the bit-wise XOR operation. To decrypt the message, Bob uses the bit-wise XOR operation: $M = M_E \oplus M_K$.

Specifically, we apply OTP to transmit randomized answers as follows. At first, each randomized answer is concatenated with the associated query identifier $Q_{ID}$ to build a message $M$: $$\begin{equation} \label{eq:message} M = Q_{ID}, RandomizedAnswer \end{equation}$$

Thereafter, $(n-1)$ random $l$-bit key strings $M_{K_i}$ with $2 \leq i \leq n$ are generated using a cryptographic pseudo-random number generator (PRNG) seeded with a cryptographically strong random number. The XOR of all $(n-1)$ key strings together forms the pseudo one-/time pad $M_K$. $$\begin{equation} M_K = \bigoplus_{i=2}^n M_{K_i} \end{equation}$$

Next, it performs an XOR operation with $M$ and $M_K$ to produce an encrypted message $M_E$. $$\begin{equation} M_E = M \oplus M_K \end{equation}$$

As a result, the message $M$ is split into $n$ messages $\langle M_E, M_{K_2}, \cdots, M_{K_n}\rangle$. Then, a message identifier $M_{ID}$ is generated and sent together with the split messages to the $n$ proxies as follows: $$\begin{equation} \label{eq:transmit} \begin{split} Client \longrightarrow Proxy1: \langle M_{ID}, M_E \rangle\\ Client \longrightarrow Proxyi: \langle M_{ID}, M_{K_i} \rangle \end{split} \end{equation}$$

Upon receiving the messages (either $\langle M_{ID}, M_E \rangle$ or $\langle M_{ID}, M_{K_i} \rangle$) from clients, proxies immediately transmit the messages to the aggregator. There are two main data streams at proxies: (i) $\langle M_{ID}, M_E \rangle$ stream and (ii) $\langle M_{ID}, M_{K_i} \rangle$ stream. $M_{ID}$ is used to ensure that $M_E$ and all $M_{K_i}$ will be joined later to decrypt or rebuild the message $M$ at the aggregator. In fact, due to pseudo one-/time pad encryption being semantically secure, $\langle M_{ID}, M_E \rangle$ and all $\langle M_{ID}, M_{K_i} \rangle$ are computationally indistinguishable, which hides from the proxies if the received data stream even contains the answer $M$ or is just a pseudo-random bit string.

Step IV: Generating Result at the Aggregator

At the aggregator, all data streams ($\langle M_{ID}, M_E \rangle$ and $\langle M_{ID}, M_{K_i} \rangle$) are received, and can be joined together to obtain a unified data stream. Specifically, the associated $M_E$ and $M_{K_i}$ are paired by using a reduce operator with the common identifier $M_{ID}$. To rebuild the original randomized message $M$ from the client, the XOR function is performed over $M_E$ and $M_K$: $M = M_E \oplus M_K$ with $M_K$ being the XOR of all $M_{K_i}$: $M_K = \bigoplus_{i=2}^n M_{K_i}$. As the aggregator does not know which of the received messages is $M_E$, it just XORs all $n$ received messages to recover $M$.

The joined answer stream is processed to produce the query results as a sliding window computation. For each window, the aggregator first adapts the computation window to the current start time $t$ by removing all old data items, with $timestamp < t$, from the window. Next, the aggregator adds the newly incoming data items into the window. Then, the answers in the window are decoded and aggregated to produce the query results for the analyst. Each query result is an estimated result which is bound to a range of error due to the approximation. The aggregator estimates this error bound and defines a confidence interval for the result as: $queryResult \pm errorBound$. The entire process is repeated for the next window, with the updated window parameters.